Let me throw some numbers at you. In 2013 (a long time ago) Sports betting was worth up to £625 billion a year, with 70% of that trade reckoned to come from football. During the 2018 football World Cup, bookmakers were estimated to make a profit north of £28 billion. There is a lot of money in the industry which has paved the way for London based companies Starlizard and Mustard Systems who utilise the fact that odds often reflect the market rather then the true probabilities. This leaves enough wiggle room for both the bookies and betting experts to make a profit at the expense of 28 year old Dave who highly overestimates his teams ability and aimlessly places a £50 bet after 6 pints in the pub. The nature of this kind of market is particularly clear with Betfair which acts like an exchange. They happily take a small cut out of every transaction whilst the users fight for the rest. The key is to accurately predict the actual probabilities in each fixture, in the light of this we find the games where sufficiently many Daves have placed a bet for us to make a profit. That sounds easy enough, but how do we do it?
The Poission Distribution
Firstly I should clarify the connection to Fantasy Premier League. In my last post we arbitrarily placed a difficulty value on each fixture to discuss which “middle men” were the most attractive to own ahead of the next few gameweeks. The aim in this post will be to put some reasoning behind that difficulty value. In summary, if we can produce a model which tells us that Brighton have a 95% probability of losing against Man City at the Etihad, this gives us incentive to stock up on City players and lose Lewis Dunk.
The Poisson distribution is a discrete probability distribution which takes positive integer values (0, 1, 2…) with some probability depending on some parameter . Here is the same thing written in the language of mathematics:
The distribution is often used to model events which:
- Have x as the number of event which occur in some time interval.
- Occur independently. That is, the occurrence of one event does not affect the probability that a second event will occur.
- The average rate at which an event occurs is constant. (It is actually equal to ).
The above assumptions seem to fit quite nicely to the goals scored by any team in a game of football. Hence, it is a Poisson distribution we will use in this post. The key is to find λ, which is the average number of goals we expect a team to score in a particular game. If the Poisson distribution is new to you, an easy example how it may be applied to football modelling is here, a good taster of what is to come. To get a feel of what probabilities the distribution gives, I have plotted the probabilities for different and x ranging from 0 to 20.
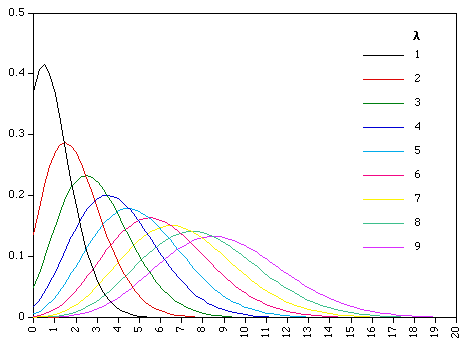
Granted a team is unlikely to be expected to score 9 goals in any game, but I hope the trend above is clear: The probability to score more goals increases as increases. If we expect a team to score 1 goal in a game, it is pretty unlikely the team will score more than 3 goals. Whilst if we expect a team to score 3 goals, they may well score 5 or 6. The simplest way to find lambda is simply to take:
As I write this on the 10th of April, Chelsea have scored 57 goals in 33 games. Using the formula above, this equates to an average scoring rate of 1.73 goals per game. Taking this value for gives the following probability values:
However, given that Chelsea face Liverpool away at Anfield in their next fixture, it is probably not reasonable to assume that there is only a 17.7% chance that they will leave the game goalless. A 25.1% change that they will score 3 or more seems a little optimistic. Clearly there are some parameters we are missing. Here are three of them:
- In football there is something called Home field advantage, discussed here. Playing on you home pitch is generally seen as an advantage which is also what data from this years Premier League season suggests. To date, the average goal scoring rate is 1.58 for home teams and 1.25 for away teams. This is a significant difference and should be taking into account in our model.
- The opposition is also important. With our example for Chelsea above, not only are they playing away from home, the fact that they are playing Liverpool makes the numbers derived from our simplistic model look a little off. The goal scoring rate clearly depends on if you’re playing Brighton or Liverpool.
- It is probably reasonable to postulate that a teams current form has some effect on their scoring rate in upcoming fixtures. This will be taken into account by only considering games played in the last 3 months.
Building the Model
We want to predict future results, so a good place to start is to look at previous results. There are a number of sources to extract this information, I get it from football-data.co.uk. Lets see what it looks like in R.
library(dplyr)
# Picking the columns we are interested in and only the games played in the last 3 months
Last_Fixture <- as.Date(gsub("/", ".", DF_Original$Date[nrow(DF)]), "%d.%m.%Y")
DF_Recent <- DF_Original[c("HomeTeam", "AwayTeam", "FTHG", "FTAG", "Date")] %>%
mutate(Date = as.Date(gsub("/", ".", Date), "%d.%m.%Y")) %>%
filter(Date > (Last_Fixture - 90))
# Creating the dataframe which we will use to build our model
ModelDF_Recent <- data.frame(Team = c(DF_Recent$HomeTeam, DF_Recent$AwayTeam),
Opposition = c(DF_Recent$AwayTeam, DF_Recent$HomeTeam),
HA = c(rep("H",nrow(DF_Recent)),rep("A",nrow(DF_Recent))),
Goals= c(DF_Recent$FTHG, DF_Recent$FTAG))
DF_Original is the dataset taken from football-data.co.uk and it contains 62 columns, most of which we are not interested in. The first few lines of code above extract the columns we want, formats the Date column, and removes games which were played more than 90 days ago.
Our aim is to build a model which takes a team, an opposition and returns a value for depending on whether the team is playing at home or away. To train such a model, we need a dataframe with the following columns “Team”, “Opposition”, “HA” and “Goals scored by Team”, where “HA” indicates if the Team is playing at home or away. Such a dataframe is built in the last few lines of code above in ModelDF_Recent and is displayed below:
| Row Num | Team | Opposition | HA | Goals |
|---|---|---|---|---|
| 1 | Brighton | Liverpool | H | 0 |
| 2 | Burnley | Fulham | H | 2 |
| ... | ... | ... | ... | ... |
| 116 | Liverpool | Brighton | A | 1 |
| 117 | Fulham | Burnley | A | 1 |
| ... | ... | ... | ... | ... |
The game between Brighton and Liverpool on the 12 Jan (86 days before the most recent fixture) appears as our first entry above. Note that the first entry relates to Brighton scoring 0 goals against Liverpool at home. The conjugate entry in line 116 says that Liverpool scored 1 goal against Brighton away. Each fixture has two conjugate entries.
Next we use this dataframe to train the model.
# Creating the Model for recent fixtures
attach(ModelDF_Recent)
Model_Recent <- glm(Goals ~ Team + HA + Opposition, family=poisson(link=log))
summary(Model_Recent) # Printing the summary
detach(ModelDF_Recent)
| Coefficients | Estimate | Std. Error | z value | Pr(>|z|) |
|---|---|---|---|---|
| (Intercept) | -0.132610 | 0.423617 | -0.313 | 0.754249 |
| TeamCrystal Palace | -0.110139 | 0.331803 | -0.332 | 0.739934 |
| TeamMan City | 0.264142 | 0.306663 | 0.861 | 0.389048 |
| HAH | 0.430247 | 0.115717 | 3.718 | 0.000201 |
| OppositionCrystal Palace | 0.472469 | 0.422454 | 1.118 | 0.263400 |
| OppositionMan City | -0.743706 | 0.606242 | -1.227 | 0.219918 |
The glm (general linear model) takes the observations in our dataframe to estimate the parameters (, ’s, ’s and ) in the following expression:
At this stage there would have been room to input a “Current Form” variable into the GLM. This could have been done rather than only considering the most recent fixtures. I explored this option and the code for this is on my GitHub page. However, this varable came out with a very large p-value and actually increased the AIC of the model.
Man City face Crystal Palace away two gameweeks from now. Reading from what we have from the table, we have:
As expected, the model predicts City to score more goals than Palace.
Next we want to make predictions for upcoming matches. SimulateMatch, defined below, takes a home and away team and reruns a matrix with probability values for final scores. The default, set in Max, is to display results up to 5 goals scored per team.
# Function that takes a home team and away team and returns a matrix with score probabilities
SimulateMatch <- function(Team, AwayTeam, Max = 5)
{HomeLambda <- predict(Model_Recent, data.frame(HA = "H", Team = Team, Opposition = AwayTeam), type = "response")
AwayLambda <- predict(Model_Recent, data.frame(HA = "A", Team = AwayTeam, Opposition = Team), type = "response")
return(dpois(0:Max, HomeLambda) %o% dpois(0:Max, AwayLambda))}
SimulateMatch("Crystal Palace", "Man City", Max = 4)
## [,1] [,2] [,3] [,4] [,5]
## [1,] 0.0904638944 0.1654968919 0.1513820591 0.0923140310 0.0422203944
## [2,] 0.0518701575 0.0948925525 0.0867993944 0.0529309882 0.0242083156
## [3,] 0.0148706468 0.0272047300 0.0248845038 0.0151747761 0.0069402780
## [4,] 0.0028421755 0.0051995463 0.0047560895 0.0029003027 0.0013264714
## [5,] 0.0004074114 0.0007453285 0.0006817613 0.0004157436 0.0001901429
At the end of the code above we have simulated the Palace - City fixture (note that we have set Max=4). The model reckons a 0-1 City win is the most likely outcome with probability of 16.5%.
The output from SimulateMatch can be used to place probabilities on a home/away win or draw by noting that the digonal entries of the matrix correspond to draws, the lower diagonal entries correspond to a home win and the upper diagonal entries an away win. An alternative approach is to use the Skellam distribution which takes two poisson parameters, for example and , and returns the difference between two independent poisson distributions with these parameters. Ie, the Skellam distribution returns Palace goals - City goals. Using this reasoning we define the following functions to calculate the probabilities we want.
library(skellam) # Includes the skellam distribution
# Function which return the probabilty of a draw
PDraw <- function(Team, AwayTeam)
{HomeLambda <- predict(Model_Recent, data.frame(HA = "H", Team = Team, Opposition = AwayTeam), type = "response")
AwayLambda <- predict(Model_Recent, data.frame(HA = "A", Team = AwayTeam, Opposition = Team), type = "response")
Answer <- dskellam(0,HomeLambda,AwayLambda)
return(percent(Answer))}
# Function which return the probabilty of a home win
PHomeWin <- function(Team, AwayTeam)
{HomeLambda <- predict(Model_Recent, data.frame(HA = "H", Team = Team, Opposition = AwayTeam), type = "response")
AwayLambda <- predict(Model_Recent, data.frame(HA = "A", Team = AwayTeam, Opposition = Team), type = "response")
Answer <- pskellam(0,HomeLambda,AwayLambda, lower.tail = FALSE)
return(percent(Answer))}
# Function which return the probabilty of an away win
PAwayWin <- function(Team, AwayTeam)
{HomeLambda <- predict(Model_Recent, data.frame(HA = "H", Team = Team, Opposition = AwayTeam), type = "response")
AwayLambda <- predict(Model_Recent, data.frame(HA = "A", Team = AwayTeam, Opposition = Team), type = "response")
Answer <- pskellam(-1,HomeLambda,AwayLambda)
return(percent(Answer))}
At this stage we have good machinery to predict the outcome of future fixtures, so lets do exactly that. The Fixtures dataframe below contains all the remaining Premier League fixtures. In the code below, we use our functions to predict the outcomes.
Fixtures <- Fixtures %>% transform(HomeWinPercentage = PHomeWin(HomeTeam,AwayTeam),
DrawPercentage = PDraw(HomeTeam,AwayTeam), AwayWinPercentage = PAwayWin(HomeTeam,AwayTeam))
| HomeTeam | AwayTeam | HomeWinPercentage | DrawPercentage | AwayWinPercentage |
|---|---|---|---|---|
| Brighton | Cardiff | 44.9% | 31.2% | 24.0% |
| Man United | Man City | 19.5% | 30.9% | 49.6% |
| Watford | Southampton | 60.1% | 21.3% | 18.6% |
| Wolves | Arsenal | 35.3% | 27.3% | 37.4% |
| Tottenham | Brighton | 70.6% | 20.9% | 8.5% |
| Burnley | Cardiff | 75.5% | 15.9% | 8.7% |
| ... | ... | ... | ... | ... |
Conclusion
We have successfully built a model which quantifies the difficulty of upcoming fixtures taking into account home field advantage, the opposition and current form. Given the conditions of the Poisson distribution it is deemed to model football scores quite well. However, there are a few point to consider.
- The Poisson distribution, and in particular the Skellam distribution, assumes that the goal scoring rate for each team is independent and constant throughout the game. Ie, if team 1 were to score 10 goals in the first 5 minutes, this would not effect the future scoring rate of either team.
- It does not account for the teams motivation. Ie, it does not capture the scenario when a team is playing for a draw. This is particularly common in the group stages of knockout competitions.
Next we need to use the derived probabilities and see how they translate to the expected points scored by any given player. If we think Spurs are pretty likely to beat Brighton in their next game, how many FPL points do we expect Mr Kane to get? Of course this is a crucial question in FPL.
We should also like to refine the model. Most likely we will consider a Dixon-Coles model which has the benefit of:
- Introducing an interaction term to correct the underestimated frequency of low scoring matches
- Applying a time decay component so that more recent fixtures are weighted more strongly
The second point is something we have already discussed in this post. Current form is something we wish to consider and it will be nice for us if this can be included naturally in the model rather than somewhat arbitrarily deciding to only consider games in the last 3 months….
Stay tuned!

Leave a comment